Recently we’ve been investigating the basics of Pylearn2. Now it’s time for a more advanced example: a multilayer perceptron with dropout and maxout activation for the MNIST digits.

Maxout explained

If you’ve been following developments in deep learning, you know that Hinton’s most recent recommendation for supervised learning, after a few years of bashing backpropagation in favour of unsupervised pretraining, is to use classic multilayer perceptrons with dropout and rectified linear units. For us, this breath of simplicity is a welcome change.

Rectified linear is f(x) = max( 0, x ). This makes backpropagation trivial: for x > 0, the derivative is one, else zero.

Note that ReLU consists of two linear functions. But why stop at two? Let’s take max. out of three, or four, or five linear functions… And so maxout is a generalization of ReLU. It can approximate any convex function.

Now backpropagation is easy and dropout prevents overfitting, so we can train a deep network. In this case just a tad deeper than usual: two hidden layers.

Data

Pylearn2 provides some code for reproducing results from the maxout paper, including MNIST and CIFAR-10.

Then there’s the digit recognizer competition at Kaggle, based on MNIST digits data (that’s why there’s no shortage of 100% scores there). Both datasets are basically the same, only the training/test split is different. We’ll run maxout code on data from this contest. An advantage of this approach is that we can hope that the provided MNIST hyperparams will work nicely with the Kaggle digits.

The Kaggle digits are a bit harder than MNIST, because they have fewer training examples: 42k, instead of 60k. Additionally, we split the training set for validation and train the model on 38k examples, without further re-training on the full set, which would probably increase accuracy.

For more info about running a multilayer perceptron on MNIST, see the tutorial by Ian Goodfellow.

Simple vs convoluted

The authors of the paper report two scores for MNIST: one for permutation invariant approach and another, better scoring, for a convolutional network.

Permutation invariant means that we don’t take advantage of the knowledge that we’re dealing with images. In other words, we could shuffle the columns in the data and the result would be the same.

If we account for the fact that a row in data is in fact a sequence of pixel rows, we can apply convolution, and that results in improved accuracy. However this makes things slightly more complicated, so for now we stick with permutation invariance.

Code

The code is available at Github. Here are two YAML snippets responsible for loading data. We use DigitsDataset class from digits_dataset.py:

dataset: &train !obj:digits_dataset.DigitsDataset {
    path: '/path/to/train_v.csv',
    one_hot: 1
}

'valid' : !obj:digits_dataset.DigitsDataset {
    path: '/path/to/test_v.csv',
    one_hot: 1,
    expect_headers: 0
}   

A dataset object corresponds to a file, so we need to specify a path. Other options (all boolean) are: one_hot for one-hot encoding, expect_headers if there’s a header line in a file and expect_labels if there are labels. In this case we have a training set with headers and a validation set without them.

Prediction is done using the predict.py script, which is basically the same as in Pylearn2 in practice.

Results

On raw data the score is very, very bad. We needed to scale X from 0…255 to 0…1, as it is in the original example:

>>> import numpy as np
>>> from pylearn2.datasets.mnist import MNIST
>>>
>>> train = MNIST( 'train' )
>>>
>>> train.X.shape
(60000, 784)
>>> np.max( train.X )
1.0
>>> np.min( train.X )
0.0

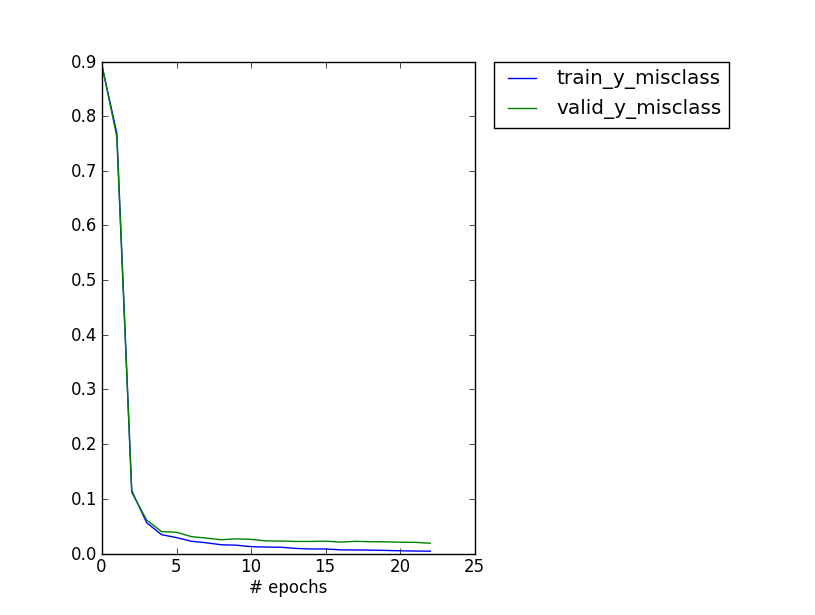
Error on the validation set goes down pretty fast with training, here’s a plot for both sets. Training stops when the validation score stops to improve.

> print_monitor.py digits_best.pkl
(...)
valid_y_misclass : 0.0154101476073

The score at Kaggle is .984. Not quite good as we hoped for, still pretty good though, in top 10%.

When to stop training

We did change some hyperparams after all: to make things quicker, initially we modfied the so called termination criterion from this:

termination_criterion: !obj:pylearn2.termination_criteria.MonitorBased {
    channel_name: "valid_y_misclass",
    prop_decrease: 0.,
    N: 100
}

to this:

termination_criterion: !obj:pylearn2.termination_criteria.MonitorBased {
    channel_name: "valid_y_misclass",
    prop_decrease: 0.001
    N: 10
},

It means “Stop training if the validation error doesn’t decrease in 10 epochs from now”. The original version waits 100 epochs and is OK with zero decrease. Here’s the relevant documentation snippet:

prop_decrease : float
    The threshold factor by which we expect the channel value to have decreased
N : int
    Number of epochs to look back

It might make a difference because during training validation error can go down, then up, and then further down. With the original settings training runs for 192 + 100 epochs and results in

valid_y_misclass : 0.0123281171545

We also changed a number of units in hidden layers from 240 each to 480 each. But surprise, surprise: the Kaggle score for the new submission is 0.98171, worse than before.

With 240 hiddens training consists of 150 + 100 epochs and validation error is 0.013. At Kaggle it scores 0.98229 - better than with 480 hidden units, still worse than the first attempt.

The reason for that might be the validation set - we use 4k examples. With such low error rate it might be not enough.

Trying to improve the score

A faster way to improve the score would be to use 4k outstanding validation examples for training. There’s no labels in the test set, so this time the termination criterion is different:

termination_criterion: !obj:pylearn2.termination_criteria.MatchChannel {
    channel_name: "valid_objective",
    prev_channel_name: "train_objective",
    prev_monitor_name: "monitor_stage_0"
}

Basically we train until a value of the objective (cost) function on the validation set (which is now again just a part of the training set) matches the value of the objective on the training set from the previous run.

Unfortunately, the Kaggle score is again slightly worse than the first attempt: 0.98243.