Now that we have Spearmint basics nailed, we’ll try tuning a random forest, and specifically two hyperparams: a number of trees (ntrees) and a number of candidate features at each split (mtry). Here’s some code.
We’re going to use a red wine quality dataset. It has about 1600 examples and our goal will be to predict a rating for a wine given all the other properties. This is a regression* task, as ratings are in (0,10) range.
We will split the data 80/10/10 into train, validation and test set, and use the first two to establish optimal hyperparams and then predict on the test set. As an error measure we will use RMSE.
At first, we will try ntrees between 10 and 200 and mtry between 3 and 11 (there’s eleven features total, so that’s the upper bound). Here are the results of two Spearmint runs with 71 and 95 tries respectively. Colors denote a validation error value:
- green: RMSE < 0.57
- blue: RMSE < 0.58
- black: RMSE >= 0.58
Turns out that some differences in the error value, even though not that big, are present, so a little effort to choose good hyperparams makes sense. A number of trees is on the horizontal axis and the number of candidate features on the vertical.


As you can see, the two runs are pretty similar. The number of trees doesn’t matter so much as long as it is big enough - good results can be achieved with less than a hundred tress.
However, mtry parameter is clearly very important - most of good runs used a value of three. This is close to a default setting, which is a square root of number of features (3.31, or 3 after rounding). If three is so good, we might try setting the lower bound to two or even one. Let’s do this, and also let’s try a limit of 300 trees. Here is the plot of the third, final run with 141 tries:
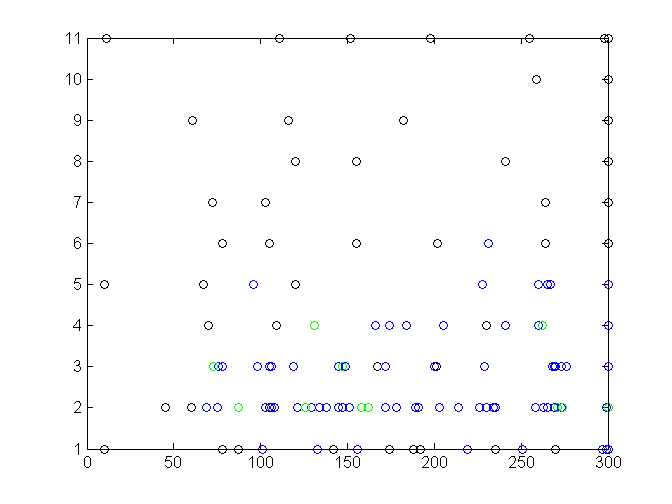
It seems that two is even better for mtry than three. And indeed, a best found combination is 158 trees, mtry 2. It produced a validation error of 0.562856. Random forests are intrinsically random, so in another run with these settings you will probably get a worse result than that or a lower error with a different number of trees. Let’s see how the error depends on mtry (we omit a few outliers to get a close-up):

The best value for mtry is probably two, three being a runner up. So maybe we discovered a better than default value for this hyperparam after all. To verify this, we will train ten random forests with the default setting and ten forests with mtry = 2. For training we’ll use all but the test set examples. Here are the results:

Oops… Specifics differ from run to run, but the pattern stays the same. Default is better. At least we got some practice.
If you’d like to learn more about impact of mtry on random forest accuracy, there’s a whole paper on this subject by Bernard et al. It can be summarised in two points:
- mtry value equal to a square root of a number of features is very sensible and often produces near-optimal results
- sometimes there are gains to be made by setting the parameter much higher, but don’t expect a dramatic improvement
There was a dramatic improvement in one case out of 12, for Madelon data set. It’s an artificial dataset prepared for NIPS 2003 Feature Selection Challenge. Most features in this dataset are just noise.
* Concretely, so called ordinal regression, but we will treat it as regular regression.