We took a look at a few videos from the 2014 International Conference on Learning Representations and here are some things we consider interesting: predicting class labels not seen in training, benchmarking stochastic optimization algorithms and symmetry-based learning.

Predicting class labels not seen in training

Can a multiclass model predict labels it haven’t seen in training? People at Google think it can. Note that we’re talking many, many classes here. For example, images from the ImageNet - a thousand classes.

The trick is to embed labels in a vector space, so that each label is represented by a vector of numbers, and semantically similiar classes are close to each other. For example, words like orange and lemon and grapefruit would be close to each other, as would be tiger and lion and puma and cheetah. Embeddings come from word2vec or something similiar.

When a classifier outputs a probability for each class, you take a number of most probable labels, let’s say 10, and use the probability estimates to produce a weighted average of the corresponding label vectors.

Then you retrieve the nearest neigbours of the resulting vector, and these are your predictions. They include classes not seen in training. For example, if the classifier haven’t seen grapefruit in training, it may think that it’s a lemon or an orange, and the idea is that a weighted average of these things is close to a grapefruit in the embedding space. As often is in machine learning, this should work as long as we’re interpolating between known points.

More in this short talk by Daniel Nourouzi, and in the paper, Zero-Shot Learning by Convex Combination of Semantic Embeddings, ConSE for short.

The same group of authors also have an earlier method to achieve similiar goal, called DeViSE - A Deep Visual-Semantic Embedding Model. It’s covered in the talk as an alternative and the conclusion is that ConSE works better. DeViSE caught the eye of the Register in December 2013.

Benchmarking stochastic optimization algorithms

Tom Schaul (a student of Juergen Schmidhuber, now in DeepMind) talked about testing SGD and various alternatives to ideally find a robust algorithm which “just works” in a variety of settings:

Each unit test rapidly evaluates an optimization algorithm on a small-scale, isolated, and well-understood difficulty, rather than in real-world scenarios where many such issues are entangled.

A possible application is to check what case your problem is similiar to and then choose a well-performing method. In the paper they present the results visually, here’s a part of one of the maps:

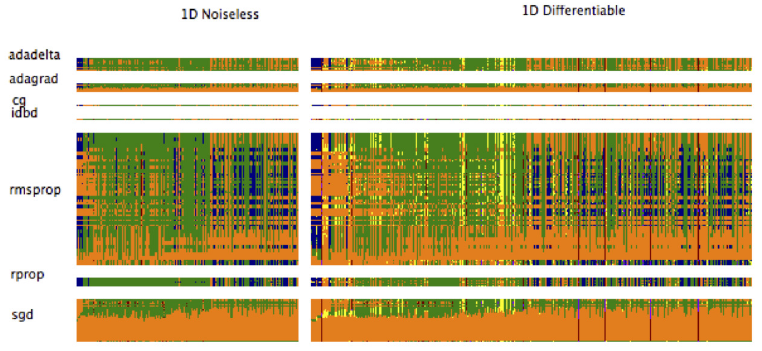
The color code is: red/violet=divergence, orange=slow, yellow=variability, green=acceptable, blue=excellent

You can see that SGD is sensitive to hyperparam settings (large orange areas), while adadelta is less sensitive, but sometimes not as good as well-tuned SGD. Rmsprop and rprop look especially good with their large green and blue areas.

The Torch testbed for the experiments, optimBench, is available at GitHub.

UPDATE: Take a look at Alec Radford’s animated visualizations of six popular stochastic optimization algorithms.

Symmetry-based learning

Pedro Domingos’ invited talk was about a nascent area of research, symmetry based learning. Mathematically, an object is symmetric with respect to a given mathematical operation, if, when applied to the object, this operation preserves some property of the object [Wikipedia].

Let’s take face images as a concrete example. A face can be rotated to the left or to the right, pitched up or down, be well illuminated or in the shadow, but it’s still the same face. And if we care about recognizing a person in the image, the transformations mentioned are symmetries because they preserve the identity of the subject.

One can think of convolutional neural networks for object recognition in images as a particular application of symmetry-based learning. Recall that convnets slide a feature map across the image so that it covers nearly all possible locations. By doing that they provide invariance to one particular form of symmetry: translation.

Translation means shifting the object either horizontally or vertically; a bee is still a bee, whether in the upper left or lower right corner. Pedro’s idea in the context of images is to extend the symmetry group to all linear transformations, for example rotations. Then a network wouldn’t need to learn rotations by itself, just as it doesn’t need to learn translations (because they are taken care of explicitly). That would make learning easier.