Last time we explored dimensionality reduction in practice using Gensim’s LSI and LDA. Now, having spent some time researching the subject matter, we will give an overview of other options.
UPDATE: We now consider the topic quite irrelevant, because sparse high-dimensional data is precisely where linear models shine. See Amazon aspires to automate access control, Predicting advertised salaries and Predicting closed questions on Stack Overflow.
And the few most popular methods are:
- LSI/LSA - a multinomial PCA
- LDA - Latent Dirichlet Allocation
- matrix factorization, in particular non-negative variants: NMF
- ICA, or Independent Components Analysis
- mixtures of Bernoullis
- stacked RBMs
- correlated topic models, an extension of LDA
We tried the first two before.
As regards matrix factorization, you do the same stuff as with movie recommendations (think Netflix challenge). The difference is, now all the matrix elements are known and we are only interested in factors for each row, because we represent a row by these factors. Non-negative part helps with interpretation.
ICA seems like an extension of PCA. There’s a popular algorithm called FastICA and indeed it’s pretty fast, at least on adult dataset. The original authors offer a Matlab implementation with and without a GUI.
There’s a couple of things to tweak, we only reduced dimensionality first to a desired number as it seems to work better than running ICA on original data.
RBMs, or Restriced Boltzmann Machines, we haven’t tried yet. They are a cornerstone of the deep learning craze a la Geoff Hinton.
A mixture of Bernoullis is a Bayesian, that is probabilistic, technique. Bernoulli is a fancy word for binary. The idea is that each example comes from one of a handful of Bernoulli distributions, or components - a component is like a topic in LDA.
The downside of this method is that each row is supposed to come from exactly one component. Therefore it will give you a row of probabilities that an example (row) comes from a given component (columns), which might be OK after all. Also, as is often the case with Bayesian methods, probably not the fastest. We have used the aspect Bernoulli model. The code is available as a single Matlab file.
We also tried Blei’s correlated topic model, which we think of as improved LDA. Results are on par with other methods.
TF-IDF
For some of the techniques, specifically LSI, PCA, ICA and NMF, TF-IDF preprocessing makes sense. The supervised score apparently is better when these techniques are applied on TF-IDF transformed data. For numbers, refer to the updated results.
TF-IDF is available in Gensim and scikit-learn - see Topics extraction with Non-Negative Matrix Factorization. We provide a script using Gensim.
With binary data TF-IDF effectively becomes IDF, because term frequency is always either one or zero. Inverse document frequency means that rare features weigh more than frequent ones.
Note that after TF-IDF data is no longer binary, because ones become floats. This means that the distinction between methods for binary/continuous data blurs. For example, you can just apply vanilla PCA.
The sparsity stays the same, meaning that zeros are still zeros. For example, here’s a “before” snippet in libsvm format:
-1 3:1 11:1 14:1
And after:
-1 3:0.262910 11:0.5400270 14:0.269577
Here are some visualizations of the impact on principal components:
Principal components of adult as shown by FastICA
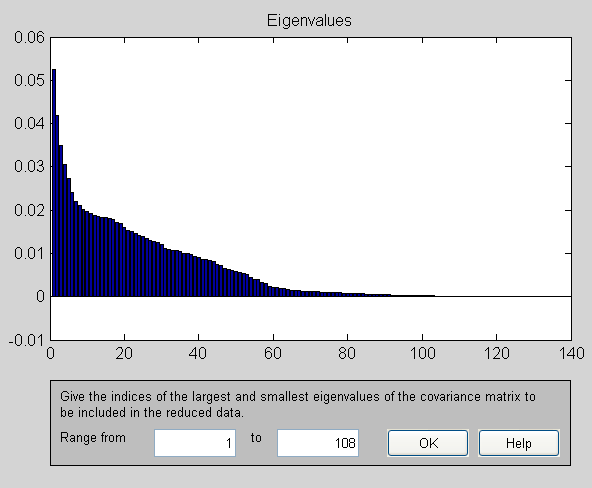Principal components for data pre-processed with TF-IDF
Conclusions
To sum up, one guy called LiangJie Hong, a research scientist at Yahoo! Labs, reviewed a few papers on binary matrix decomposition and his punch line is this:
In all, it seems that the performance advantages of specifically designed binary data models are small. (…) For computational models, NMF seems a good approximation. For probablistic models, a modified PLSA or LDA seems quite resonable.
We would generally agree. All methods we have tried seem to be rather close to each other as regards the supervised score they achieve. The main difference is in speed and scalability. As far as scalability goes, online methods have the upper hand here, because some data sets are too big to fit in memory.
Overall, for big data LSI in Gensim might be a good first choice. It’s online and reasonably fast. For even bigger data, probably LDA in VW. Vowpal Wabbit has built-in super-fast LDA, which is interesting. Unfortunately, in our experience it is not as easy to get it to work as with Gensim. It’s a skill to learn.
An additional advantage of LSI/PCA is that once you decompose the data, you can take as many components as you want, without re-running. For example, you train 100 and then use first 10 or first 20 or first 50 or all 100, because they are linearly uncorrelated. This is in contrast to other methods, in which you train specifically for a chosen number of topics.
SPAMS is worth mentioning, as it is much faster than Gensim. The algorithms, both NMF and non-negative sparse coding, are online, but apparently need whole data in memory. They benefit from TF-IDF preprocessing. We provide a script for doing NMF with SPAMS.
Randomized PCA from scikit-learn is also amazingly fast and offers a similiar quality of results.
Finally, we would like to mention Graphlab/Graphchi, one of a few tools on par with Vowpal Wabbit for large scale learning. Graphlab is about parallelization and many machines, Graphchi about out-of-core learning on one machine. Danny Bickson wrote a few matrix factorization routines for both, including NMF and RBMs. Unfortunately, for some reason the scores from Graphchi seem to be significantly lower than from other methods.